DNN Gradient Vanishing or Exploding

DNN Gradient Vanishing or Exploding

build 2 hidden layer DNN with an output layer

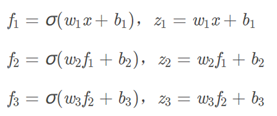
loss is function of f3

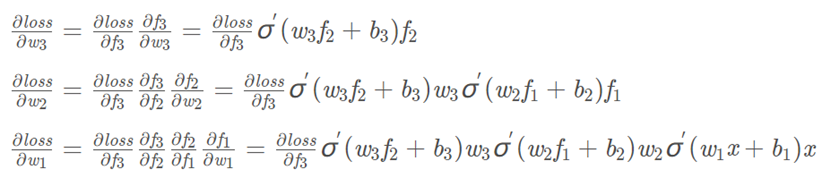
根据上面规律，我们可以把x写成f0，当有n-1层隐层时，fn是输出，如果要求wl也就是第l层的权重，反向传播中涉及的偏导计算为：

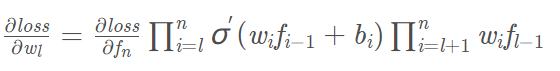
前半部分是关于激活函数的导数的累乘，后半部分是关于权重值的累乘。

激活函数如sigmoid函数，其导数的取值范围是(0, 0.25]，当网络层数很深的时候，多个小于1的数进行累乘，结果是趋向于0的，此时梯度反向传播的时候，根据参数更新公式：$w {l} = w{l}-lr·\frac{\partial loss}{\partial w _{l}}$ ，偏导部分的取值趋于0，那么该参数得不到更新，这就是梯度消失现象。消失的只是更新参数所需要的梯度，而不一定是参数被更新到0。

关于权重值的累乘，当我们初始化权值很大的时候，多个大于1的数累乘，结果是+∞，此时就出现了梯度爆炸现象。

NN: detach()

detach()是生成了一个新的variable，detach_()是对本身的更改，

detach()

（1）返回一个新的从当前图中分离的Variable。

（2）返回的 Variable 不会梯度更新

（3）被detach()的相当于**with torch.no_grad()**操作

（4）返回的Variable和被detach的Variable指向同一个tensor

x = torch.tensor([1], requires_grad=True)
with torch.no_grad():
	y = x * 2

>>> y.requires_grad
False

NN: detach_()

Detach_()

（1）将一个Variable从创建它的图中分离，并把它设置成叶子Variable。

（2）将中间节点的grad_fn的值设置为None时，这样中间节点就不会再与前一个节点关联，此时的中间节点就变成了叶子节点。

（3）将中间节点的requires_grad设置为False，这样对后面节点进行backward()时就不会对中间节点求梯度